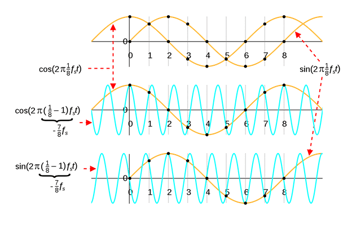
Filtrado en el dominio de la frecuencia
En este blog, mostraré dos aplicaciones sencillas derivadas del Teorema de Convolución:
-
- Analizar una señal y aplicar un filtro en el dominio de la frecuencia.
- Generar un filtro personalizado en el dominio de la frecuencia.
El Teorema de Convolución establece que la convolución en el dominio del tiempo es equivalente a la multiplicación en el dominio de la frecuencia y viceversa. Cuando convolucionamos dos señales, estamos esencialmente filtrando una señal.
Veamos la señal de impulsos de barro de la figura 1.
.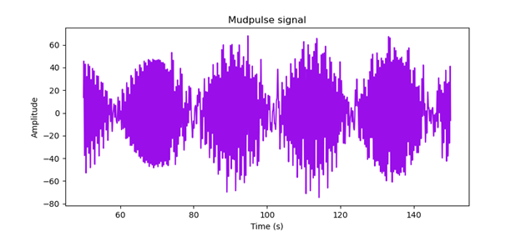
Figura 1. Señal de pulso de lodo. Señal de pulso de lodo.
Parece haber muchas interferencias de ruido eléctrico. Si tomamos la transformada de Fourier o miramos el contenido de frecuencia de nuestra señal, podemos ver que hay grandes componentes de frecuencia alrededor de 0,84, 1,68 y 2,55 Hz, como se muestra en la Figura 2. Esos componentes de frecuencia son probablemente ruido contaminando nuestra señal. Esos componentes de frecuencia son probablemente ruido que contamina nuestra señal.
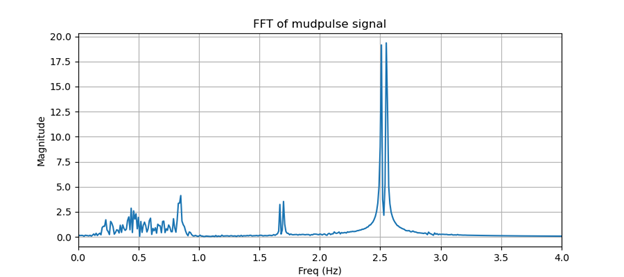
Figura 2. FFT de la señal mudpulse FFT de la señal mudpulse.
Eliminemos esas frecuencias o apliquemos filtros de supresión a nuestra señal. Podemos hacerlo enmascarando esta señal en el dominio de la frecuencia y aplicando una transformada de Fourier inversa para obtener nuestra señal filtrada en el dominio del tiempo. La Figura 3 muestra nuestra máscara de frecuencias y la Figura 4 muestra nuestra señal de frecuencias enmascarada.
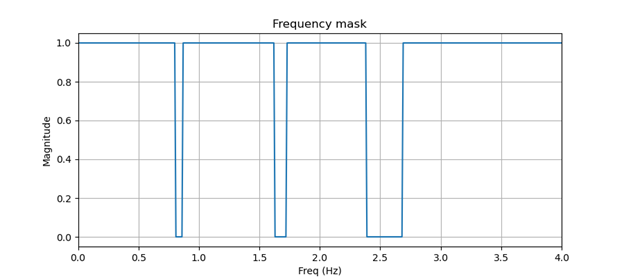
Figura 3. Máscara de frecuencia. Máscara de frecuencia.
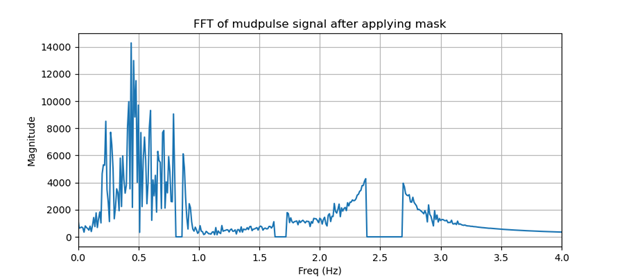
Figura 4. FFT de la señal mudpulse tras aplicar la máscara.
Después de convertir nuestra señal de frecuencia enmascarada de nuevo al dominio del tiempo, ahora podemos ver claramente nuestra señal mudpulse se muestra en la Figura 5.
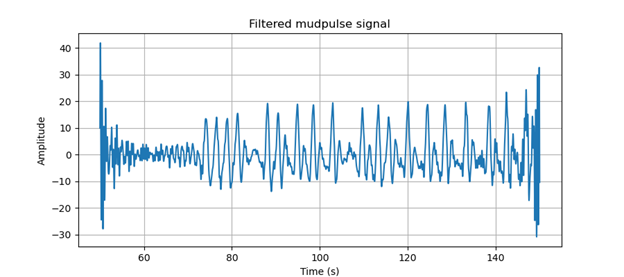
Figura 5. Señal de impulso de lodo filtrada. Señal de impulso de lodo filtrada.
En el dominio de la frecuencia, es fácil ver que sólo estamos eliminando el componente de frecuencia correspondiente al ruido en nuestra señal de impulsos de lodo, pero ¿qué ocurre en el dominio del tiempo?
Al definir una máscara de frecuencia, estamos diseñando nuestro propio filtro personalizado. Si tomamos la transformada inversa de Fourier de nuestra máscara de frecuencia, podemos ver que nuestra máscara de frecuencia no es más que un simple filtro FIR como el que se muestra en la figura 6. Si convolucionamos este filtro y nuestra señal de impulso de lodo, obtendremos la misma señal de impulso de lodo filtrada que se muestra en la Figura 5.
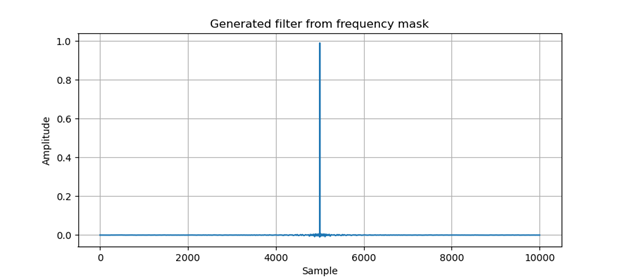
Figura 6. Filtro generado a partir de la máscara de frecuencia. Filtro generado a partir de la máscara de frecuencia.