Filtering in the Frequency Domain
In this blog, I will be showcasing two simple applications derived from the Convolution Theorem:
-
- Analyzing a signal and applying a filter in the frequency domain.
- Generating a custom filter in the frequency domain.
The Convolution Theorem states that convolution in the time domain is equivalent to multiplication in the frequency domain and vice versa. When we convolve two signals, we are essentially filtering a signal.
Let us look at this mud pulse signal in Figure 1.
.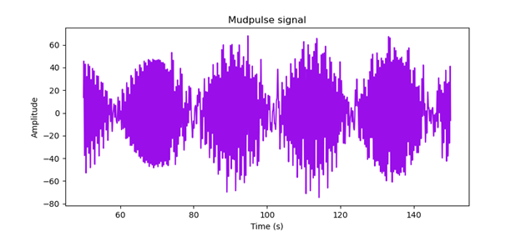
Figure 1. Mudpulse signal.
There seems to be a lot of electrical noise interference. If we take the Fourier transform or look at the frequency contents of our signal, we can see there are large frequency components around 0.84, 1.68, and 2.55 Hz shown in Figure 2. Those frequency components are probably noise contaminating our signal.
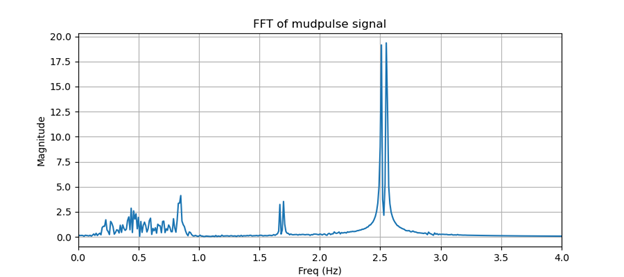
Figure 2. FFT of mudpulse signal.
Let us zero out those frequencies or apply notch filters to our signal. We can do this by masking out this signal in the frequency domain and applying an inverse Fourier transform to obtain our filtered time domain signal. Figure 3 shows our frequency mask and Figure 4 shows our masked frequency signal.
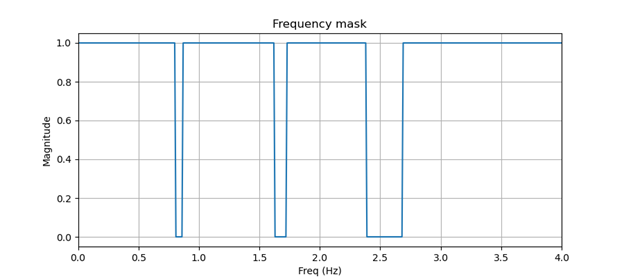
Figure 3. Frequency Mask.
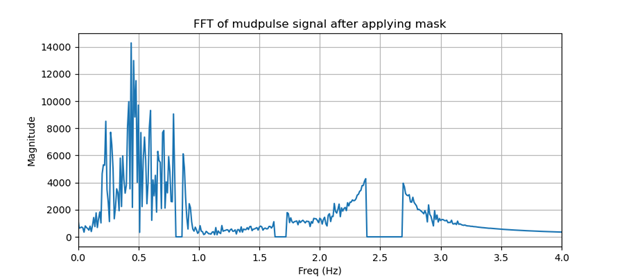
Figure 4. FFT of mudpulse signal after applying mask.
After converting our masked frequency signal back to the time domain, we can now clearly see our mudpulse signal show in Figure 5.
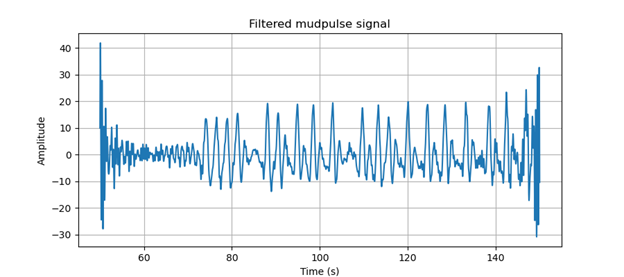
Figure 5. Filtered mudpulse signal.
In the frequency domain, it is easy to see we are just removing the frequency component corresponding to noise in our mudpulse signal, but what is happening in the time domain?
By defining a frequency mask, we are designing our own custom filter. If we take the inverse Fourier transform of our frequency mask, we can see our frequency mask is just a simple FIR filter show in Figure 6. If we convolve this filter and our mudpulse signal, we get the same filtered mudpulse signal shown in Figure 5.
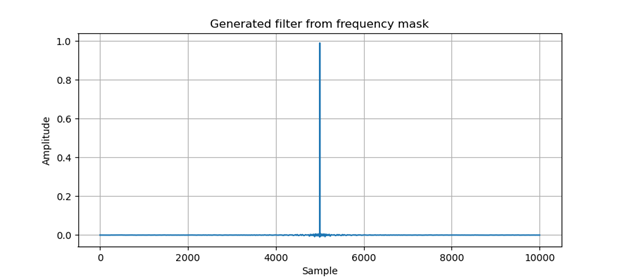
Figure 6. Generated filter from frequency mask.