Explicación de la tasa de Nyquist y el filtro antialiasing
En la telemetría de impulsos de lodo, utilizamos una señal de sincronización. Una señal de sincronización comúnmente utilizada son cuatro pulsos igualmente espaciados. La señal de sincronización nos permite alinear los datos correctamente para la descodificación. Tras la sincronización, se utilizan las ubicaciones de los pulsos para descodificar. Si la señal digital que estamos analizando está dañada por pulsos ausentes o falsos, la señal distorsionada puede dar lugar a sincronizaciones ausentes y descodificaciones falsas. Una posible fuente de distorsión es el aliasing.
El aliasing se produce cada vez que muestreamos una señal. El aliasing es un efecto que hace que diferentes señales parezcan iguales una vez muestreadas. Esto ocurre cuando no se cumple la tasa de Nyquist, que se deriva del Teorema de Nyquist. El Teorema de Nyquist establece que nuestra frecuencia de muestreo debe ser al menos el doble de la componente de frecuencia más alta de nuestra señal para obtener una representación precisa. Esta frecuencia de muestreo mínima se conoce como frecuencia de Nyquist. En la Figura 1 se muestra un ejemplo sencillo de aliasing, en el que dos sinusoides diferentes tienen el mismo aspecto tras el muestreo. Dado que cualquier señal puede representarse como o es equivalente a una suma de sinusoides, este efecto de aliasing puede causar mucha distorsión o desinformación en nuestra señal digital. Para ayudar a reducir los artefactos causados por el aliasing, se suele aplicar un filtro antialiasing o paso bajo para limitar el ancho de banda de nuestra señal.
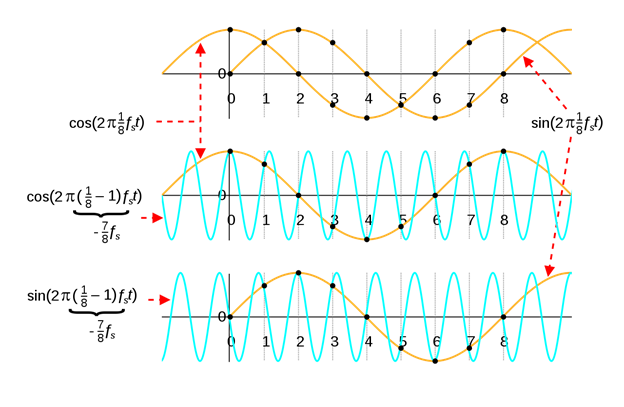
Figura 1. Aliasing Ejemplo de aliasing de dos sinusoides. https://upload.wikimedia.org/wikipedia/commons/thumb/4/47/Aliasing_between_a_positive_and_a_negative_frequency.svg/1280px-Aliasing_between_a_positive_and_a_negative_frequency.svg.png
El aliasing es un resultado del Teorema de Convolución, que establece que la convolución en el dominio del tiempo corresponde a la multiplicación en el dominio de la frecuencia (1) y viceversa (2).
F[x(t)*y(t)]=X(jω) Y(jω) (1)
F[x(t) y(t)]=X(jω)*Y(jω) (2)
Cuando muestreamos una señal x(t), esencialmente estamos multiplicando nuestra señal por un tren de impulsos p(t), donde T es nuestro intervalo de muestreo y f_s=1/T es nuestra frecuencia de muestreo.
z[n]=x(nT)=x(t) p(t) (3)
p(t)=∑_(k=-∞)^∞▒〖δ(t-kT)〗 (4)
Esta multiplicación da como resultado la convolución de sus transformadas de Fourier en el dominio de la frecuencia. Sin embargo, la transformada de Fourier de un tren de impulsos no es más que un tren de impulsos con un periodo igual a nuestra frecuencia de muestreo f_s. A título ilustrativo, digamos que x(t) está limitada en banda con la componente de frecuencia más alta de B.
Esto resulta en la transformada de Fourier de nuestra señal muestreada a ser una suma de múltiples copias de X(f) desplazado por 〖nf〗_s se muestra en la Figura 2 y 3. De esta simple ilustración se puede ver que si B es mayor que la tasa de Nyquist, f_s/2 las copias se superponen causando aliasing.
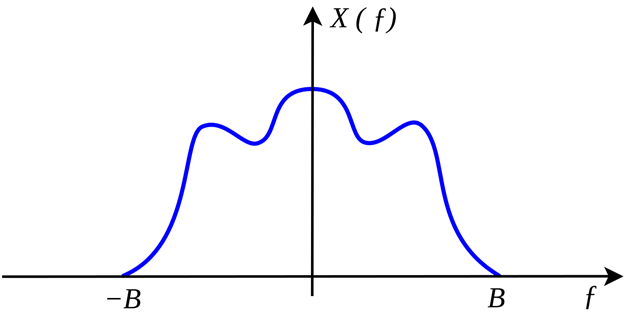
Figura 2. Transformada de Fourier de nuestra señal de ejemplo Transformada de Fourier de nuestra señal de ejemplo. https://upload.wikimedia.org/wikipedia/commons/thumb/f/f7/Bandlimited.svg/1280px-Bandlimited.svg.png
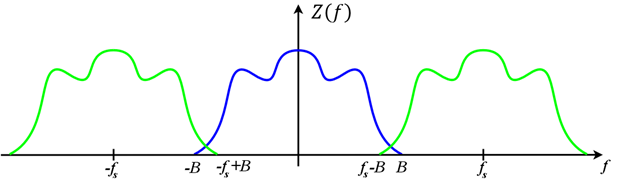
Figura 3. Transformada de Transformada de Fourier de nuestra señal muestreada. https://upload.wikimedia.org/wikipedia/commons/d/d5/AliasedSpectrum.png




