A Proportional Integral Derivative controller (PID Controller) is a closed loop control system that is commonly used in industrial control systems. This method is very effective when dealing with an application that requires continuous control modulation. In the following article, we will briefly summarize the basic function of a PID controller, the need for tuning the control loop and the effect of each term of the controller.

PID Basics

At its core, a PID controller computes an error value as defined as the difference between the current control value and a target control value. Using this error value, the control loop provides corrections to some output system. In order to control the nature of the corrections provided by the PID loop, the control loop uses 3 control terms. As its name indicates, the PID loop uses a proportional, integral and derivative term. Each term influences the aspects of the how the control system moves towards the target value. In order to tune a PID control loop to behave in a manner suitable for certain applications, each term is multiplied by a coefficient to modulate it’s influence on system behavior. In the diagram below, the 3 coefficients are Kp, Ki and Kd.

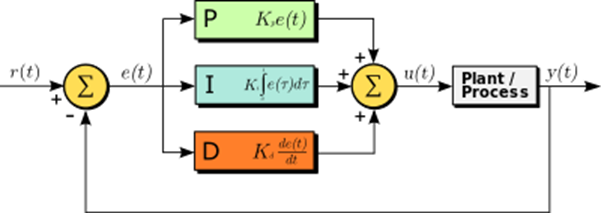
Figure 1: PID control loop block diagram

Proportional Term

Proportional term generates an output value based on a proportional value of the error value. Increasing the coefficient of the proportional term creates a more sensitive control loop. With a high coefficient, the resultant PID controller will respond more quickly and reach the given target value faster. However, this method will cause greater system instability and will cause more overshoot. Generally, the proportional coefficient is the dominate coefficient of a PID control loop and should contribute the bulk of output behavior.

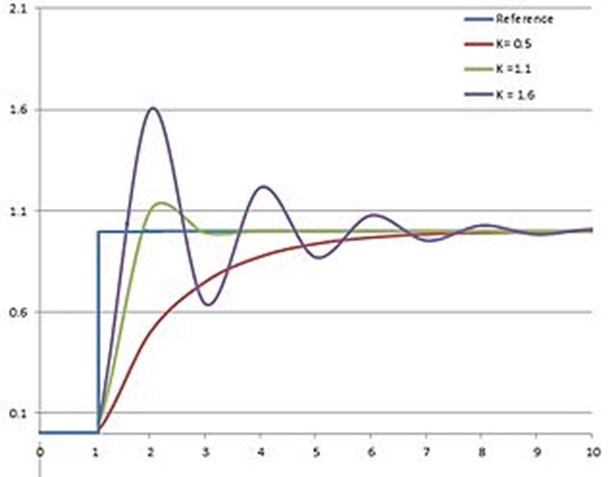
Figure 2: System responses with different Kp coefficients

Integral Term

The integral error takes the integral of errors recorded by the control loop and thus accounts for both the magnitude and the duration of the error values. Because the integral considers time, it can account for the current error value and error values detected in the past, something the proportional term alone cannot do. Higher integral coefficient helps to dampen the steady state error, or the ringing of the output value about the target value. This allows the system to settle more quickly to its target. However, high integral coefficients can cause greater overshoot when first approaching the target.

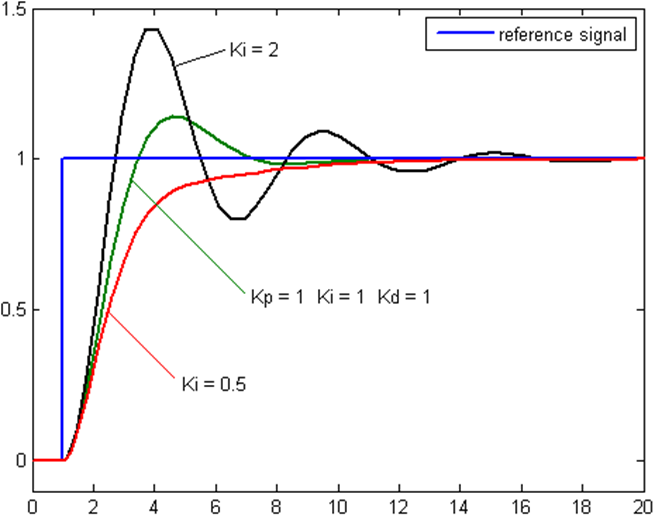
Figure 3: System responses with different Ki coefficients

Derivative Term

The Derivative term uses the slope of the error value as it changes over time. In this manner, the derivative term tracks the error as it changes over time and can be used to predict system behavior. The derivative term can greatly smooth performance of the control loop, increase settling time and stability. However, the derivative term of a PID control loop is very seldom used in practice as it’s effects on system performance can be very difficult to predict. As a result, tuning a proper derivative term coefficient is generally very difficult.

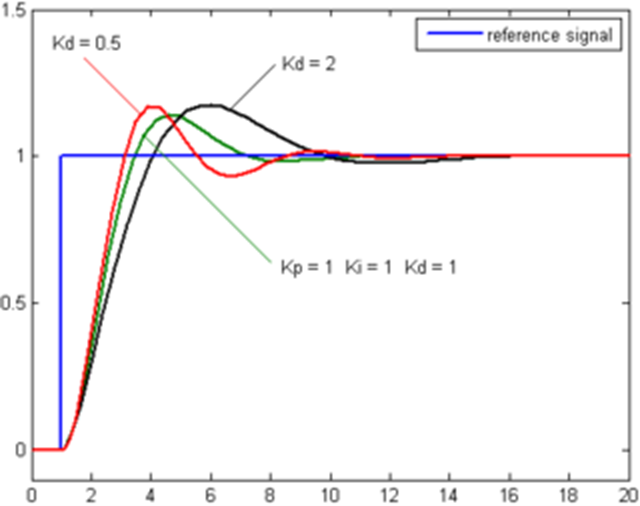
Figure 4: System responses with different Kd coefficients