Introducción

La humilde onda sinusoidal, a menudo nuestro primer viaje al reino de la acústica y a veces la pesadilla de los estudiantes de matemáticas en las escuelas de todo el mundo. En el mundo de los sistemas embebidos, las ondas sinusoidales son igualmente omnipresentes. A menudo, los sistemas embebidos necesitan generar salidas de onda sinusoidal utilizando algún tipo de circuito de digital a analógico. Aquí, revisaremos rápidamente los conceptos básicos sobre cómo generar una onda sinusoidal y los pros y los contras de las diversas opciones disponibles para los sistemas embebidos.

Conceptos básicos

Los fundamentos de una onda sinusoidal son relativamente simples. El seno es una de las relaciones trigonométricas que compara uno de los ángulos de un triángulo rectángulo con la relación entre la longitud del lado opuesto al ángulo y la hipotenusa de dicho triángulo, siendo la hipotenusa el lado opuesto al ángulo recto de 90 grados.

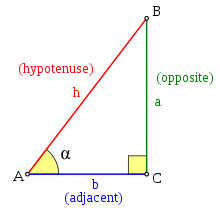
Figura 1: Relación trigonométrica del seno

Observando la relación anterior, la longitud del lado opuesto, a, depende del ángulo alfa. Si suponemos que la hipotenusa, h, tiene una longitud fija de 1, la longitud de a aumentará al aumentar alfa y viceversa. Este es el concepto detrás del Círculo Unitario, una manera de visualizar la forma en que el lado opuesto a cambia a medida que alfa cambia.

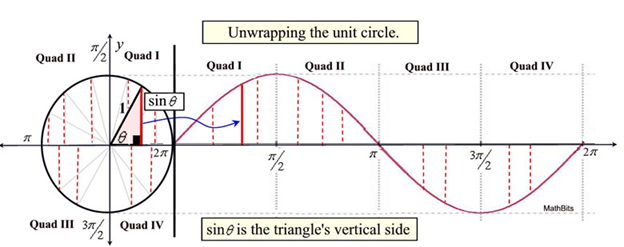
Figura 2: Círculo unitario de la onda sinusoidal

Como se muestra en la figura 2, a medida que el valor del ángulo central cambia, el valor del seno también cambiará, aumentando a medida que el ángulo aumenta hasta que el ángulo sea de 90 grados. En este caso, el lado opuesto será equivalente a la hipotenusa, resultando un valor de uno. Una vez superado este punto, si seguimos aumentando el ángulo, el valor del seno disminuirá, ya que nos encontramos en el cuadrante 2 de la circunferencia unitaria. Si seguimos trazando el valor del seno, veremos el valor del seno a medida que pasamos por los 4 cuadrantes del círculo unitario. Esta oscilación en el valor del seno a medida que atravesamos el círculo unitario es lo que produce la característica onda sinusoidal.

Métodos de generación de ondas sinusoidales

Así, considerando esta visualización de la onda sinusoidal a partir del círculo unitario, el método para generar la onda sinusoidal en firmware es esencialmente una implementación de mapeo. Debemos corresponder un valor angular y hacerlo coincidir con un punto de valor en la forma de onda sinusoidal. Para lograr esto, hay 2 métodos básicos.

Funcionalidad matemática

Un método para generar una onda sinusoidal es mediante la librería matemática proporcionada. Estas librerías proporcionan una plétora de funciones útiles para calcular valores matemáticos comunes. El seno está, por supuesto, incluido en estas librerías.

Pros

• Simplicidad de código - A menudo, estas funciones de biblioteca pueden ser importadas directamente en proyectos de código y luego simplemente llamadas. Proporcione a la función un parámetro angular de entrada y obtenga el correspondiente valor del seno que puede ser utilizado para cualquier aplicación que sea necesaria.
  
  
• Eficiencia de memoria - A diferencia del método de la tabla senoidal, la función matemática no requiere almacenar una gran tabla en memoria para calcular la correspondencia entre el ángulo de entrada y el valor del seno.
  
  
• Granularidad - Dado que la función matemática calcula el valor del seno en tiempo real cuando es necesario a partir del ángulo de entrada, el valor del seno resultante tiene una gran precisión, normalmente tanta como puede proporcionar el algoritmo utilizado por la librería en el cálculo.

Contras

• Velocidad de cálculo - Dado que el valor del seno se calcula matemáticamente cuando se llama a la función seno, los requisitos de tiempo para utilizar la tabla matemática son mucho mayores en comparación con la tabla del seno. La mayoría de las funciones seno utilizan sumas de expansión de Taylor para calcular el valor del seno con alta precisión, lo que requiere muchos cálculos. Así, cada vez que se llama a la función seno, el procesador debe emplear tiempo en calcular el resultado.
  
  
• Dependencia de librerías - El uso de la función seno requiere la inclusión de un paquete específico de librerías matemáticas en el proyecto. Esto podría afectar a la portabilidad del código durante el desarrollo, ya que una segunda máquina podría no disponer de la biblioteca, lo que requiere otro aspecto de la gestión del proyecto que no es necesario cuando se utiliza el método de la tabla senoidal.

Tabla sinusoidal

El segundo método es el uso de una tabla senoidal. Este método crea una tabla de índices en la memoria, cada entrada corresponde a un valor del ángulo senoidal de entrada mapeado a un valor senoidal de salida precalculado. Esta tabla subdivide el valor del círculo unitario de 360 grados o 2 pi radianes en partes iguales y crea una entrada en la tabla de senos para cada subdivisión. Esto significa que, por ejemplo, si se creara una tabla senoidal para valores de 1 grado, habría 360 entradas en la tabla senoidal.

Pros

• Simplicidad funcional - Aunque es un poco más trabajosa de configurar y utilizar, la tabla seno es funcionalmente más simple de utilizar que una función matemática. Dado que la tabla seno simplemente requiere el uso de acceso a memoria con un índice, es funcionalmente equivalente al uso de un array. No requiere matemáticas complejas ni llamadas a bibliotecas.
  
  
• Velocidad de cálculo - Dado que una tabla senoidal es en realidad una simple lectura de memoria, calcular un valor senoidal con una tabla senoidal es mucho más rápido que utilizar una función matemática de biblioteca.
•  

Contras

• Requerimientos de Memoria - La tabla senoidal requiere una tabla de valores para ser guardada en memoria. En función de los valores de indexación, esta tabla podría tener un tamaño considerable y limitar la disponibilidad de memoria para otras funciones.
  
  
• Valores discretos - Dado que la tabla senoidal funciona relacionando un valor angular de índice con un valor senoidal precalculado, el valor senoidal resultante puede carecer de precisión si el ángulo senoidal deseado no coincide con uno de los valores de índice preestablecidos. Esto puede mitigarse en cierta medida mediante la interpolación lineal entre los dos valores de índice y los dos valores sinusoidales de salida. Sin embargo, como las ondas sinusoidales no son funciones lineales, los resultados seguirán sufriendo una pérdida de precisión.

Créditos

Figura 1: Wikipedia - Sine : Sine - Wikipedia

Figura 2: MathBitsNotebook.com - Unit Circle and Trig Graphs : Unit Circle and Trig Graphs - MathBitsNotebook(A2 - CCSS Math)