Comparación de diferentes métodos para obtener el número 50 de Fibonacci en C++

Cuando comparamos distintos algoritmos, solemos fijarnos en la complejidad espacial y temporal, y tomamos una decisión basada en las necesidades de la aplicación. Echemos un vistazo al problema, "encontrar el número ⁵⁰ de Fibonacci", y ver cómo se podría ir sobre la comparación de diferentes soluciones a este problema. Todos los ejemplos de este post están escritos en C++ y compilados con MSVC 2019 x64. Veremos una solución a la vez, discutiremos el rendimiento y las compensaciones, y con suerte terminaremos encontrando la "mejor" solución.

Solución recursiva

La ecuación general de los números de Fibonacci se define como donde n es un número entero positivo. Esto conduce a, en mi opinión, la solución más natural.

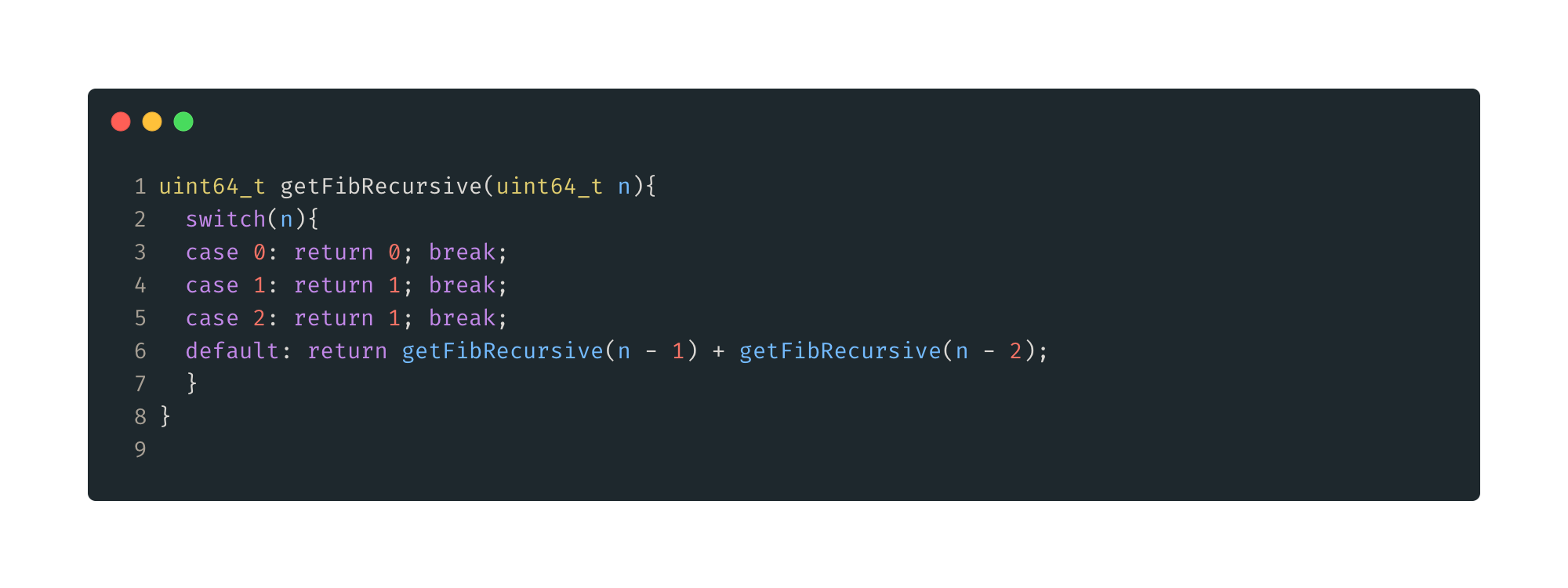
Figura 1: Solución recursiva. Aquí definimos los casos base, n<3, y luego llamamos recursivamente a la misma función siguiendo la ecuación.

El análisis de la complejidad temporal de esta función es un poco complicado, así que no voy a entrar en él aquí, pero se puede ver que a medida que n crece, la cantidad de llamadas a la función crece exponencialmente. Resulta que la complejidad temporal de esta solución es . La complejidad espacial en este caso es básicamente la profundidad de la pila de llamadas requerida, y que crecerá proporcionalmente con N, así que llamémosla .

El análisis de complejidad está muy bien, pero veamos algunos números reales para hacer esta comparación un poco más divertida. Para ello, vamos a configurar algunas funciones de ayuda y un temporizador.

Configurar

Empecemos con un temporizador. Hay muchas librerías que pueden hacer esto, pero por simplicidad, y para aquellos que nos siguen en casa, vamos a utilizar las librerías STL disponibles. Específicamente usaremos std::chrono para obtener el tiempo actual y medir duraciones.

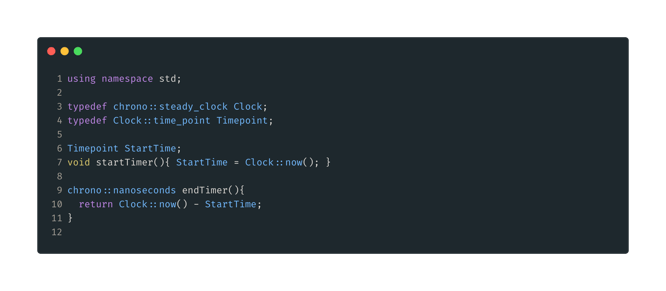
Figura 2: Funciones de cronómetro. Hemos utilizado el namespace std y un par de typedefs sólo para reducir la verbosidad. Declaramos un Timepoint "global" StartTime aquí, startTimer() lo establecerá a la hora actual. Finalmente endTimer() de nuevo obtiene el tiempo actual y lo devuelve menos el StartTime previamente adquirido, el tipo del retorno es ahora una duración.

De nuevo, por simplicidad, todo nuestro código vivirá en main.cpp. Usted podría encapsular mejor esta función para la reutilización, pero en este caso, esto es todo lo que necesitamos. Llamaremos a startTimer() justo antes de nuestra llamada a la función fib, e inmediatamente después llamaremos a endTimer().

A continuación vamos a crear una forma genérica de llamar a nuestras diversas funciones fib. En esta función también podemos encapsular una forma de obtener un tiempo de rendimiento más preciso, es decir, vamos a llamar a la función, digamos, 1000 veces y promediar el resultado.

Figura 3: Función de llamada a la función. En primer lugar, definimos algunas constantes que describirán nuestros parámetros de prueba. Aquí tenemos nuestro número Fibonacci objetivo, 50, y promediaremos los resultados de 1M de iteraciones. Luego imprimimos la duración en ms, us, y ns, y también el número resultante sólo para verificar nuestra respuesta.

Ok, ahora vamos a configurar nuestro main. Esta función, con la ayuda de una bonita macro, nos permitirá tener un cuerpo principal muy simple. Esto hará que sea natural añadir tantas funciones de prueba como queramos.

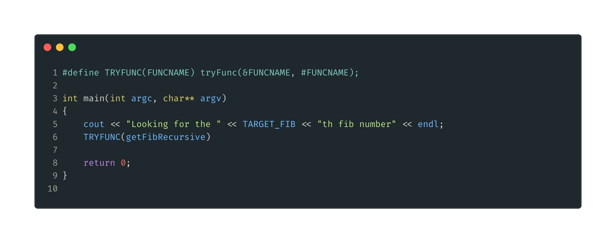
Figura 4: Configuración del main. Primero, definimos la macro TRYFUNC, que nos permitirá llamar a tryFunc() con un solo parámetro. En Main, imprimimos un texto inicial, y luego llamamos a TRYFUNC con nuestra primera función fib, getFibRecursive().

Los resultados de la solución recursiva son malos. Así que, sólo en este caso, vamos a disminuir el recuento de iteraciones a sólo 2.

Buscando el número 50 de fib
probando la función fib: getFibRecursive...
30767ms, o
30767035us, o
30767035100ns
resultado: 12586269025

Alrededor de 30 segundos para obtener el número50 de Fibonacci con la solución recursiva.

Aquí está el tryFunc() modificado con la cantidad de iteraciones del caso especial para esta función. El resultado del resto de nuestras funciones debería ser lo suficientemente rápido para hacer todas las iteraciones de 1M. Basado en este resultado getFibRecursive() tomaría alrededor de 1 año para completar esa cantidad de iteraciones.

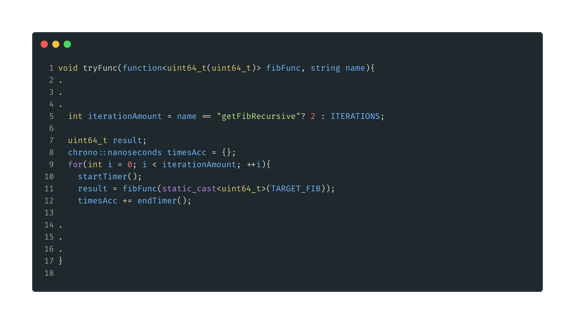
Figura 5: TryFunc() modificada. Se han omitido las secciones duplicadas, el listado completo de código se insertará al final. Aquí sólo modificamos iterationAmount basándonos en qué función está siendo llamada. Para getFibRecursive() solo haremos 2 iteraciones, todos los otros casos usaremos la cantidad de ITERACIONES, 1M.

Recursivo con Caché

Basándonos en la solución anterior, si simplemente no recalculamos un número que ya hemos visto, deberíamos ser capaces de reducir en gran medida el número de iteraciones. Esto es lo que parece.

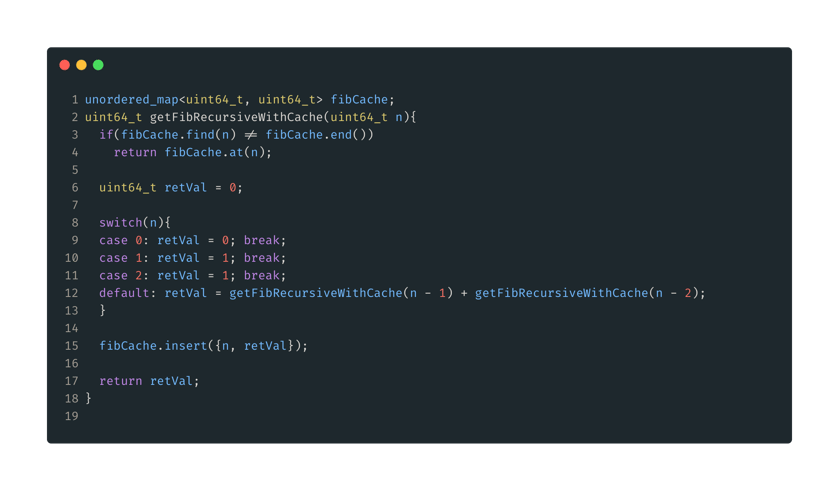
Figura 6: Recursivo con caché. Aquí, nuestra caché será un mapa que contendrá pares {n, fib(n)}. Primero, comprobamos si el número que buscamos está en la caché y, en caso afirmativo, lo devolvemos. En caso contrario, volvemos a nuestra solución recursiva anterior. Después de obtener un resultado, insertamos ese valor en nuestra caché y lo devolvemos.

La complejidad temporal ha mejorado, sólo calcularemos cada número de Fibonacci una vez hasta n, así que O(n). Nuestra complejidad espacial se ha mantenido igual, nuestra fibCache crecerá proporcionalmente a n, y todavía tenemos llamadas recursivas así que nuestra pila crecerá con n. Esto se simplifica a O(n).Veamosen los resultados de sincronización.

probando la función fib: getFibRecursiveWithCache...
0ms, o
3us, o
3741ns
resultado: 12586269025

De 30s a 3us, no está mal. Sigamos.

Solución iterativa

Ahora una solución no recursiva.

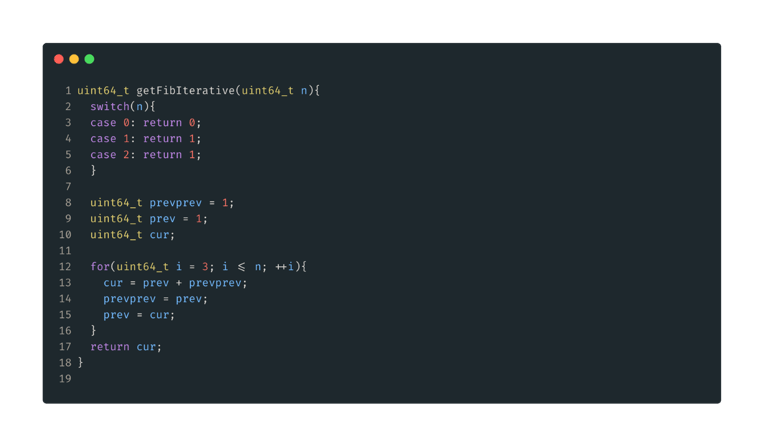
Figura 7: Solución iterativa. Comience con los tres primeros números predefinidos, a continuación, empezar a contar hasta n. Mantenga un registro de los dos números anteriores, sumarlos en cada iteración para obtener el siguiente número, a continuación, actualizar nuestros números anteriores. Finalmente devuelve el resultado una vez que alcanzamos n.

Habrá n iteraciones, por lo que la complejidad temporal es O(n). Nuestro uso de memoria es constante, no cambiará con diferentes valores de n, por lo que la complejidad espacial es
O(1). Muy bien. Y ahora los números.

probando la función fib: getFibRecursiveWithCache...
0ms, o
3us, o
51ns
resultado: 12586269025

Mejor resultado hasta ahora en 52ns. Bastante más rápido que nuestra primera solución. ¿Podemos hacerlo mejor? En resumen, sí, si torcemos un poco las reglas.

Ecuación Solución

Este es mi blogpost, así que por qué no intentar una solución directa a través de una ecuación. Hay una ecuación, creo que sólo se llama la fórmula del número de Fibonacci, que utiliza la proporción áurea , conocida como Phi(Φ)

Figura 8: Solución de la ecuación.

La complejidad espacial es obviamente O(1). La complejidad temporales interesante aquí, pow( ) aquí tardarámás proporcional a n. Así que se podría llamar a esto complejidad temporalO(n).Y el resultado.

probando la función fib: getFibEquation...
0ms, o
3us, o
218ns
resultado: 12586269025

218ns. Esto es en realidad peor que nuestra solución iterativa. Nuestra solución iterativa está haciendo básicamente n operaciones de suma. Nuestra solución de ecuación está haciendo n multiplicaciones dos veces, por lo que es comprensiblemente más lenta. También hay que tener en cuenta que para n=50, nuestra solución de ecuación es lo suficientemente precisa, pero se vuelve menos precisa para n más grandes. De todos modos, una forma en que podríamos mejorar esto es tratar de optimizar la función pow(). Hay formas más rápidas de calcular potencias, pero en general sólo se puede obtener una mejora de velocidad de 2-3x, y se perderá aún más precisión. Esta es una solución bastante mala, pero, ya que estamos rompiendo las reglas, vamos a suponer que sabemos qué número de Fibonacci queremos en tiempo de compilación. ¿Podemos forzar que este cálculo se haga en tiempo de compilación en vez de en tiempo de ejecución e inflar nuestros números de rendimiento?

Solución de la ecuación de expresión constante

Si le decimos al compilador que el tipo de retorno es constexpr, entonces tiene que ser capaz de calcularlo en tiempo de compilación.Esto significa que no podemos utilizar un argumento normal para llamar a esto, así que vamos a utilizar un argumento de plantilla.

Figura 9: Ecuación de Expresión Constante. Lo mismo que la solución de la ecuación anterior, ligeramente modificada para usar un tipo de retorno constexpr y un argumento de plantilla.

probando la función fib: getFibEquation...
0ms, o
3us, o
218ns
resultado: 12586269025

Mejor. Aunquetodavía no se acerca al rendimiento denuestra solución iterativa . Ya que estamos en el territorio de tiempo de compilación, vamosa ir un poco más lejos, y obtener un poco más de precisión de nuevo.

Solución de plantilla recursiva

Volvamos a la idea de una solución recursiva, pero esta vez usando argumentos de plantilla para forzar la evaluación en tiempo de compilación.

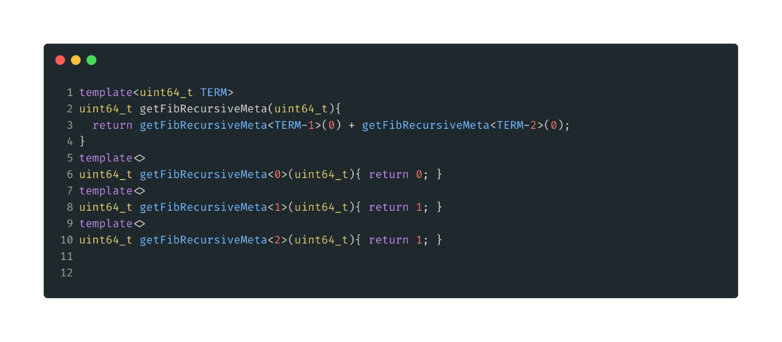
Figura 10: Solución de plantilla recursiva. Primero definimos nuestro caso general, igual que el caso general recursivo normal. Luego definimos los casos base como especializaciones de plantillas.

Fíjate que aquí mantenemos el argumento regular, pero no lo usamos, para que la firma de nuestra función cambie y podamos seguir usando nuestra macro TRYFUNC.En fin, a los números.

intentando la función fib: getFibEquation... <TARGET_FIB>...
0ms, o
3us, o
36ns
resultado: 12586269025

Fantástico. Nuestro mejor resultado. Ahora vamos a hacer una comprobación visceral, ¿cuál es el mejor absoluto que podemos hacer? Un valor codificado por supuesto.

Solucióncodificada

Esto es básicamente un punto de referencia para comparar el rendimiento de nuestro algoritmo.

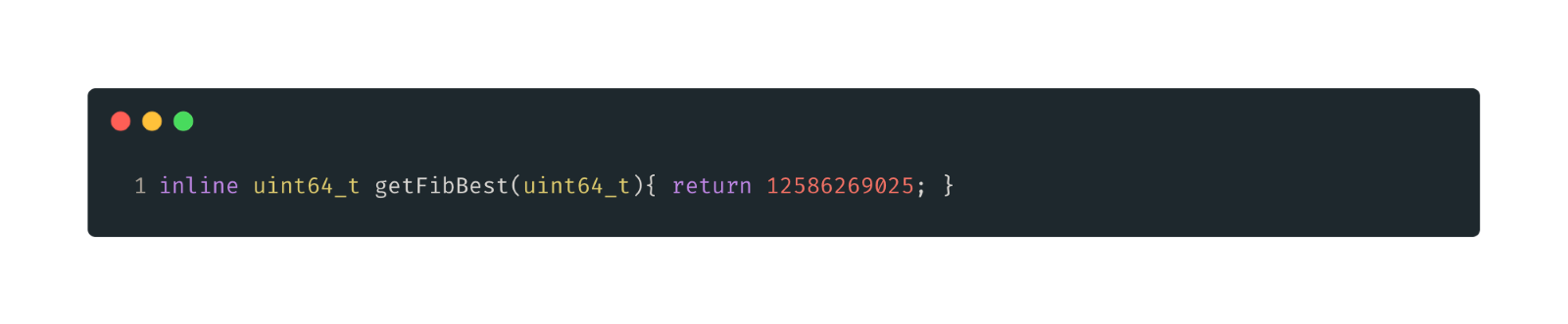
Figura 11: Solución codificada. Ya sabemos lo que es fib(50), así que devuélvelo.

probando la función fib: getFibBest...
0ms, o
3us, o
35ns
resultado: 12586269025

Impresionante. Así que nuestra solución de plantilla recursiva era básicamente tan buena como la codificación dura.Para la evaluación del compilador está funcionando como se esperaba.

Resultados

Vamos a poner todos los números juntos para verlo en un solo lugar.

Puedes ver que en algunos casos una solución O(n) supera a una solución O(1). Esto se debe a que n es pequeño (50 en este caso). A medida que n aumenta, no es de esperar que aumenten los tiempos de la solución O(1), mientras que los tiempos de las soluciones O(n) aumentarán de forma constante con n. Por lo tanto, si se utiliza un número de fibras objetivo de, digamos, 1 millón, la solución iterativa O(n) probablemente sería peor que la solución de la ecuación O(1).

(*) Tenga en cuenta que para la complejidad espacial de la plantilla recursiva solución está marcada como O(1). Esto se debe a que aquí sólo estoy hablando de memoria en tiempo de ejecución. Si tuviéramos en cuenta el tamaño del exe compilado, sería O(n), es decir, el tamaño del exe crecería proporcionalmente a n. Un tema para otro post podría ser la comparación de estas soluciones basadas en el tiempo de compilación y el tamaño del exe compilado. Estos factores podrían ser tan importantes como el tiempo de ejecución en algunas aplicaciones.

El listado completo del código utilizado está disponible gratuitamente aquí: https://pulsetoollogs.s3.amazonaws.com/blogpostfiles/FibonacciInvestigation/main.cpp

Otras soluciones

Por supuesto, hay muchas otras formas de calcular los números de Fibonacci, un par de ellas que planeaba investigar antes de que esto se alargara demasiado eran la solución de Duplicación Rápida y la solución de Duplicación Rápida Iterativa. Las encontré aquí: https://www.geeksforgeeks.org/fast-doubling-method-to-find-the-nth-fibonacci-number/

Fuentes

Su, Francis E., et al. "Fórmula de los números de Fibonacci". Math Fun Facts.<https://www.math.hmc.edu/funfacts>.

Åhlén, J. (s.f.). Proporción áurea (1,618...) a 10.000 decimales. Boxentriq. Obtenido el 18 de febrero de 2022, del sitio Web: https://www.boxentriq.com/code-breaking/golden-ratio.

https://carbon.now.sh utilizado para generar imágenes.