Comparing different methods to get the 50th Fibonacci number in C++

When comparing different algorithms, we typically look at space and time complexity, and make a trade off decision based on the applications needs. Let’s look at the problem, “find the 50^th Fibonacci number,” and see how you might go about comparing different solutions to this problem. All examples in this post are written in C++ and compiled with MSVC 2019 x64. We will look at one solution at a time, discuss the performance and tradeoffs, and hopefully end up finding the “best” solution.

Recursive Solution

The general Fibonacci number equation is defined as where n is a positive integer. This leads to, in my opinion, the most natural solution.

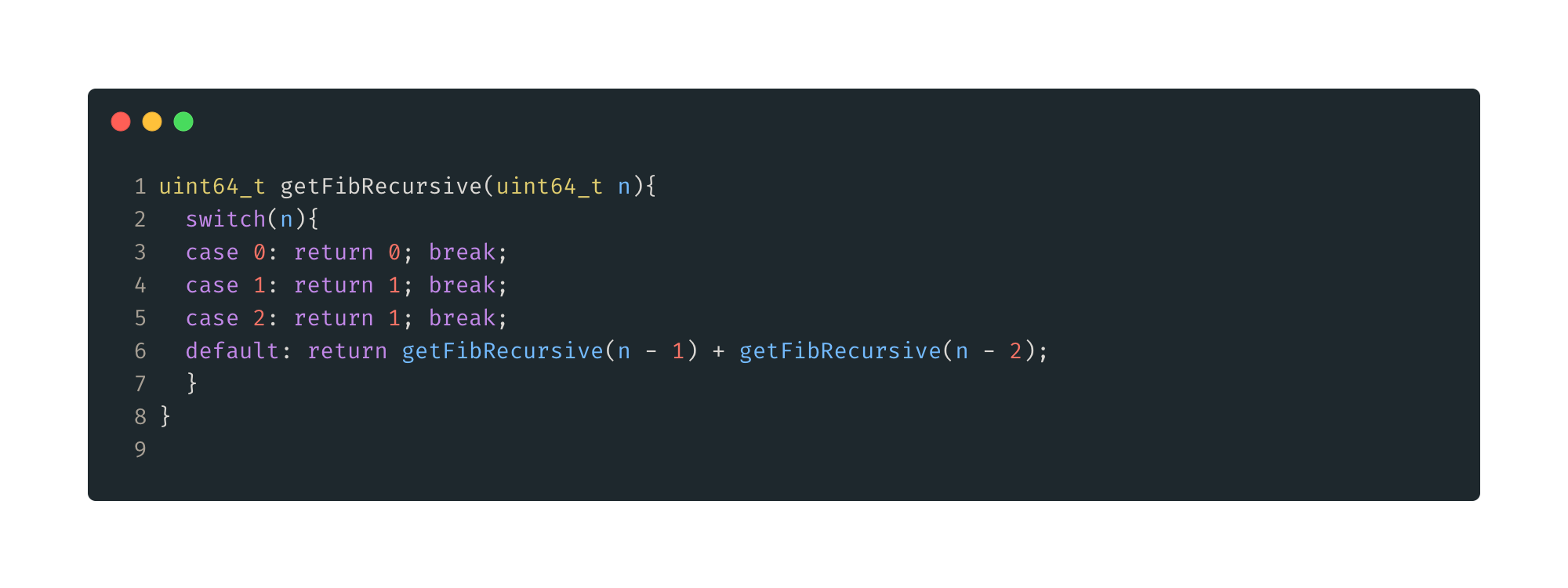
Figure 1: Recursive Solution. Here we define the base cases, n<3, then recursively call the same function following the equation.

Time complexity analysis for this function is a little tricky so I will not go into it here, but you can see that as n grows, the amount of function calls grows exponentially. It turns out that the time complexity of this solution is . The space complexity in this case is basically the depth of the call stack required, and that will grow proportional with N so let’s call that .

Complexity analysis is great and all, but let’s see some real numbers to make this comparison a bit more fun. To do this, lets setup some helper functions and a timer.

 Setup 

 Let’s start with a timer. There are many libraries that can do this, but for simplicity, and for those following along at home, let’s just use available STL libraries. Specifically we will use std::chrono to get the current time and measure durations.  

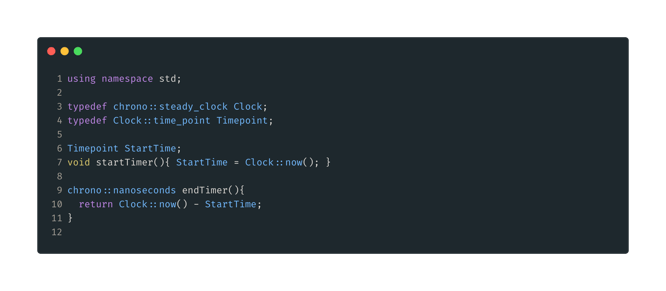
Figure 2: Timer functions. We have using namespace std and a couple typedefs just to cut down on verbosity. We declare a Timepoint “global” StartTime here, startTimer() will set this to the current time. Finally endTimer() again just gets the current time and returns that less the previously acquired StartTime, the type of the return is now a duration.  

Again, for simplicity, all our code will just live in main.cpp. You might better encapsulate this function for reusability, but in this case, this is all we need. We will call startTimer() just before our fib function call, then immediately call endTimer().  

Next let’s create a generic way to call our various fib functions. In this function we can also encapsulate a way to get a more accurate performance time, namely, let’s call the function, say, 1000 times and average the result.  

Figure 3: Function caller function. First, we define some constants that will describe our test parameters. Here we have our target Fibonacci number, 50, and we will average the results of 1M iterations. Then we print out the duration in ms, us, and ns, and also the resultant number just to verify our answer.  

Ok, so now let’s setup our main. This function, with the help of a cute macro, will allow us to have a very simple main body. This will make it natural to add as many test functions as we like. 

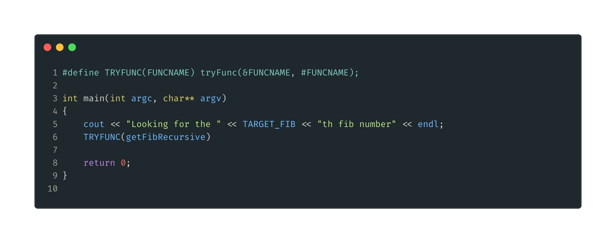
Figure 4: Main setup. First, we define the TRYFUNC macro, which will allow us to call tryFunc() with just one parameter. In Main, we print out some starting text, then call TRYFUNC with our first fib function, getFibRecursive(). 

The results of the recursive solution are bad. So, in just this case, we will decrease the iteration count to just 2.

Looking for the 50th fib number
trying fib function: getFibRecursive...
30767ms, or
30767035us, or
30767035100ns
result: 12586269025

About 30 seconds to get the 50th Fibonacci number with the recursive solution.  

Here is the modified tryFunc() with the special case iterations amount for this function. The result of the rest of our functions should be quick enough to do all 1M iterations. Based on this result getFibRecursive() would take about 1 year to complete that many iterations. 

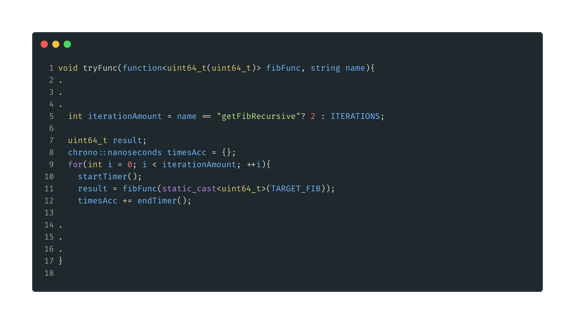
Figure 5: Modified tryFunc(). Duplicate sections omitted, full code listing will inserted at the end. Here we just modify iterationAmount based on what function is being called. For getFibRecursive() we will just do 2 iterations, all other cases we will use ITERATIONS amount, 1M. 

Recursive With Cache 

Building on the previous solution, if we simple do not recalculate a number we have already seen, we should be able to greatly reduce the number of iterations. Here is what that looks like. 

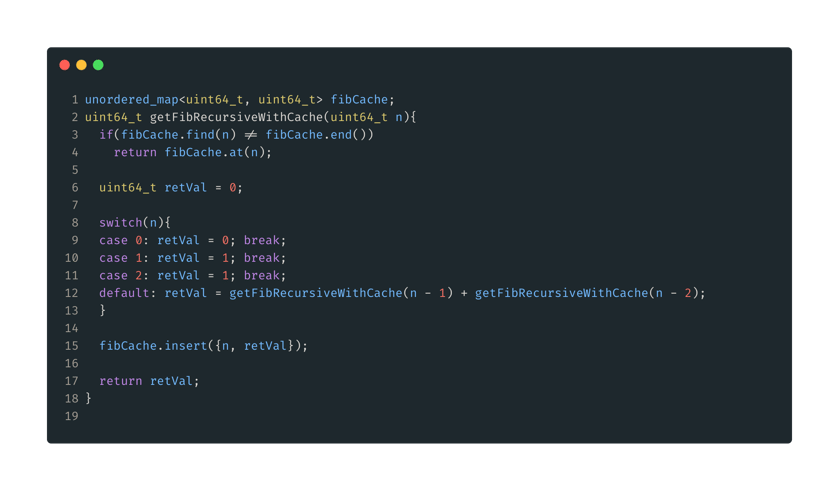
Figure 6: Recursive with cache. Here, our cache will be a map that will hold pairs {n, fib(n)}. First, we check if the number we are looking for is in the cache, if yes, return it. Otherwise, we fall back to our previous recursive solution. After we get a result, we insert that value into our cache and then return it.  

Time complexity has improved, we will only calculate each Fibonacci number once up to n, so O(n). Our space complexity has remained the same, our fibCache will grow proportional to n, and we still have recursive calls so our stack will grow with n. This simplifies to O(n). Let’s look at the timing results.  

trying fib function: getFibRecursiveWithCache... 
0ms, or
3us, or
3741ns
result: 12586269025

From 30s to 3us, not bad. Let’s move on.

Iterative Solution 

Now for a non-recursive solution.  

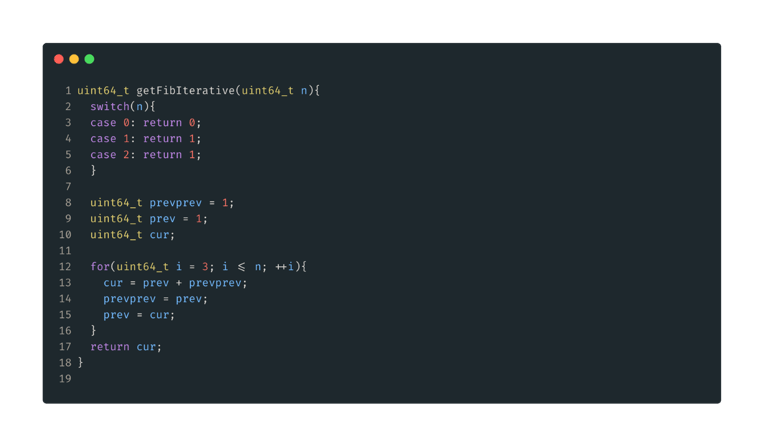
Figure 7: Iterative solution. Start with the first three numbers predefined, then start counting up to n. Keep track of the two previous numbers, add them together for each iteration to get the next number, then update our previous numbers. Finally return the result once we reach n.

There will be n iterations, so time complexity is O(n). Our memory usage is constant, will not change with different values of n, so space complexity is
O(1). Nice. And now the numbers.

trying fib function: getFibRecursiveWithCache... 
0ms, or
3us, or
51ns 
result: 12586269025

Best result so far at 52ns. Quite a bit faster than our first solution. Can we do better? In short, yes, if we bend the rules a bit. 

Equation Solution 

This is my blogpost, so why not just try a direct solution via an equation. There is an equation, I think just called the Fibonacci Number Formula, that utilizes the golden ratio, known as Phi(Φ)

Figure 8: Equation solution. 

Space complexity is obviously O(1). Time complexity is interesting here, pow( ) here will take longer proportional to n. So you could call this O(n) time complexity. And the result.  

trying fib function: getFibEquation...
0ms, or
3us, or
218ns 
result: 12586269025

218ns. This is actually worse than our iterative solution. Our iterative solution is just doing basically n addition operations. Our equation solution is doing n multiplications twice, so it is understandable slower. Also keep in mind that for n=50, our equation solution is accurate enough, but it gets less accurate for larger n. Anyway, one way we could improve this is trying to optimize the pow() function. There are faster ways out there to calculate powers, but in general you can only get a 2-3x speed improvement, and you will lose even more accuracy. This is a pretty bad solution, but, since we are already breaking the rules, let’s assume we know which Fibonacci number we want at compile time. Can we force this calculation to be done at compile time instead of runtime and inflate our performance numbers?

Constant Expression Equation Solution 

If we tell the compiler the return type is constexpr, then it has to be able to compute it at compile time. This means we cannot use a regular argument to call this, so let’s use a template argument. 

Figure 9: Constant Expression Equation. Same thing as the previous equation solution, slightly modified to use a constexpr return type and a template argument. 

trying fib function: getFibEquation...
0ms, or
3us, or
218ns 
result: 12586269025

Better! Still not approaching our iterative solution performance though. Since we are in compile time territory, let’s go a little further, and get some more accuracy back.   

Recursive Template Solution  

Let’s go back to the idea of a recursive solution, but this time use template arguments to force compile time evaluation.  

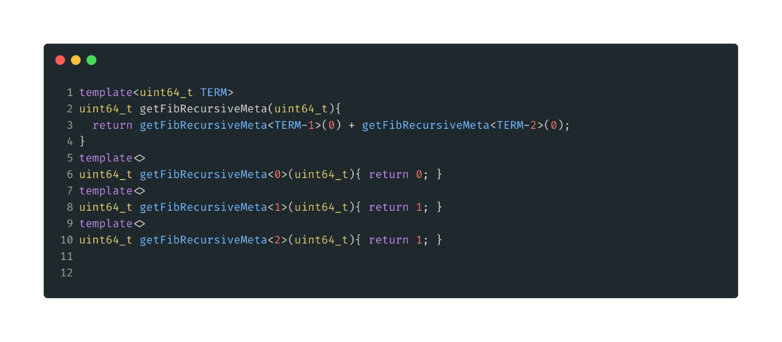
Figure 10: Recursive Template Solution. First we define out general case, same as the normal recursive general case. Then we define are base cases as template specializations.  

Notice here we are keeping the regular argument, but not using it, so that our function signature does change and we can still use our TRYFUNC macro. Anyways, on to the numbers.  

trying fib function: getFibEquation... <TARGET_FIB>...
0ms, or
3us, or
36ns 
result: 12586269025

Fantastic. Our best yet. Now let’s do a gut check, what is the absolute best we can do? A hard coded value of course. 

Hard Coded Solution 

This is basically just a benchmark to compare our algorithm performance to. 

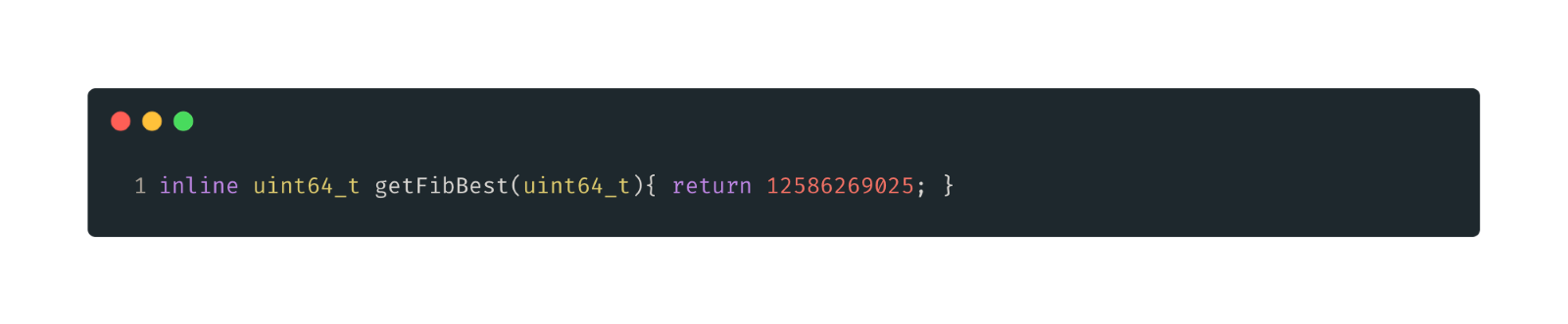
Figure 11: Hard coded solution. We already know what fib(50) is, so just return it. 

trying fib function: getFibBest...
0ms, or
3us, or
35ns 
result: 12586269025

Awesome. So our recursive template solution was basically just as good as hard coding. To the compiler evaluation is working as expected. 

Results 

Let’s just put all the numbers together to see it in one place.  

You can see that in some cases an O(n) solution is outperforming an O(1) solution. This is just because we have small n(50 in this case). As n increases you would not expect any O(1) solution times to increase, whereas O(n) solutions times will steadily increase with n. So if you used a target fib number of say 1 Million, the iterative O(n) would probably be worse than the equation O(1) solution.  

(*) Note that for the space complexity of the Recursive Template solution is marked as O(1). This is because I am only talking about runtime memory here. If we took onto account compiled exe size, it would be O(n), ie the exe size would grow proportional to n. A topic for another post might be comparing these solutions based on compile time and compiled exe size. Those could be just as important as runtime factors in some applications.  

Full code listing used freely available here: https://pulsetoollogs.s3.amazonaws.com/blogpostfiles/FibonacciInvestigation/main.cpp 

Other solutions 

Of course, there any many other ways to calculate Fibonacci numbers, a couple I planned to investigate before this got too long were the Fast Doubling solution and the Iterative Fast Doubling solution. I found those here: https://www.geeksforgeeks.org/fast-doubling-method-to-find-the-nth-fibonacci-number/ 

Sources 

Su, Francis E., et al. “Fibonacci Number Formula.” Math Fun Facts. <https://www.math.hmc.edu/funfacts>. 

Åhlén, J. (n.d.). Golden Ratio (1.618...) to 10,000 decimals. Boxentriq. Retrieved February 18, 2022, from https://www.boxentriq.com/code-breaking/golden-ratio 

https://carbon.now.sh used to generate images.