Linear phase and computation/memory complexity are important characteristics to consider when designing digital filters. When a filter has linear phase, all input frequency components are shifted in time by the same amount. This helps with preserving the waveform’s shape, which is an important aspect of mudpulse decoding.
Shown below is an example of two different filters with the similar magnitude response. Filter A has linear phase, while filter B has non-linear phase. From the frequency response, you can tell a filter has linear phase if the phase response has a constant slope.
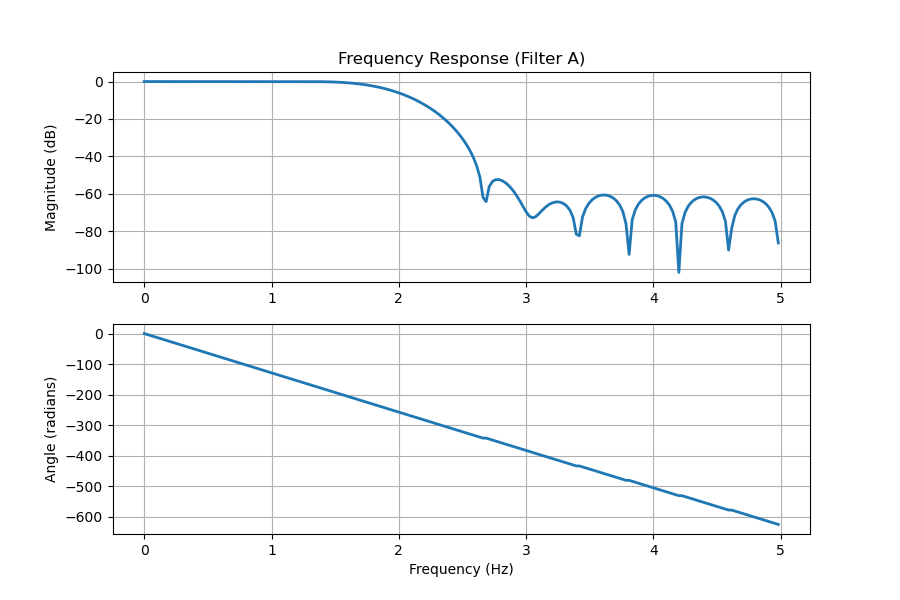
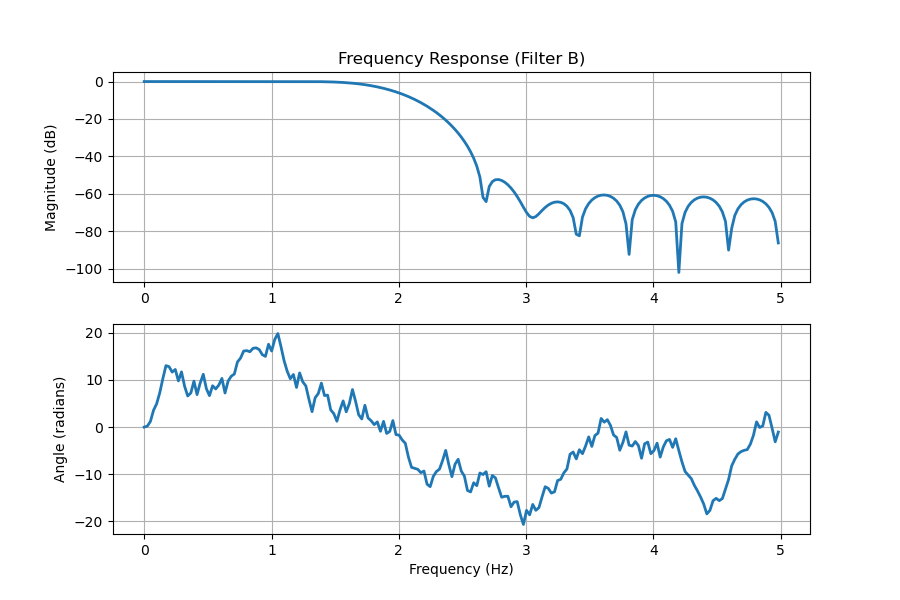
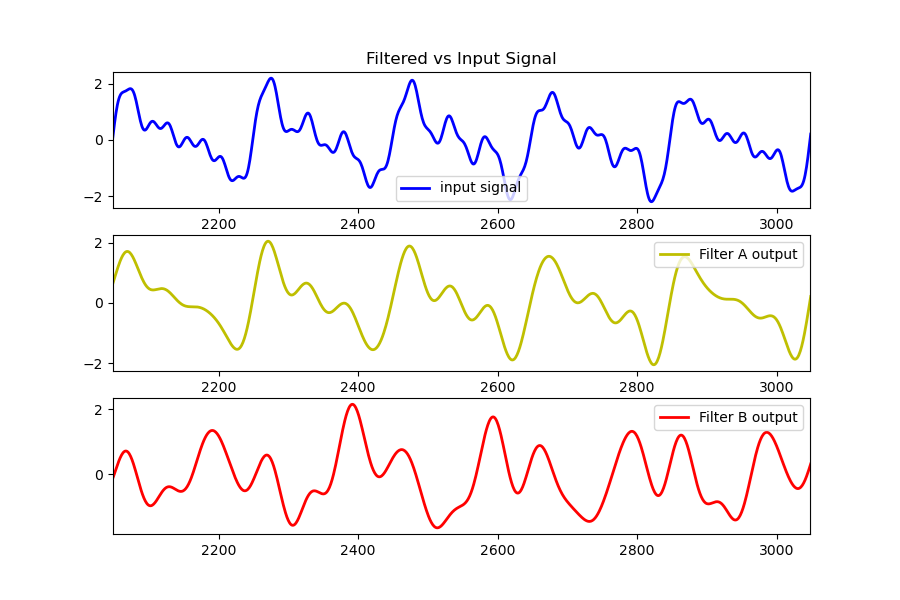
Although this is an extreme case, you can easily see that the waveform’s shape is highly distorted using filter B.
A linear phase, digital IIR filter cannot be realized due to the requirements for linear phase. Whereas, a linear phase, digital FIR filters can easily be generated. Specifically, the transfer function of a linear phase filter would need to satisfy . This suggests that an IIR filter must have poles outside the unit circle to have linear phase. However, this means the IIR filter would not be BIBO stable.
Linear phase is nice to have. However, if time delay or computation/memory complexity is important, we can always generate IIR filters with close to linear phase in the passband or frequency range of our desired signal. Shown below is a simple example of two different lowpass filters with a 1 Hz cutoff, one is a 1st order IIR filter, and the other is an 84 tap FIR filter. Both filters produce very similar outputs with the IIR filter having a lot less complexity and delay.
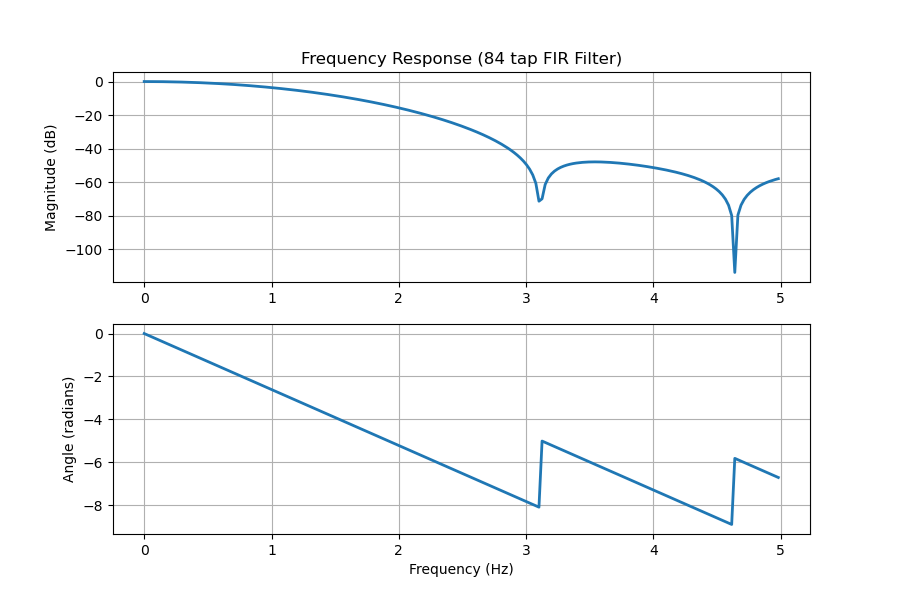
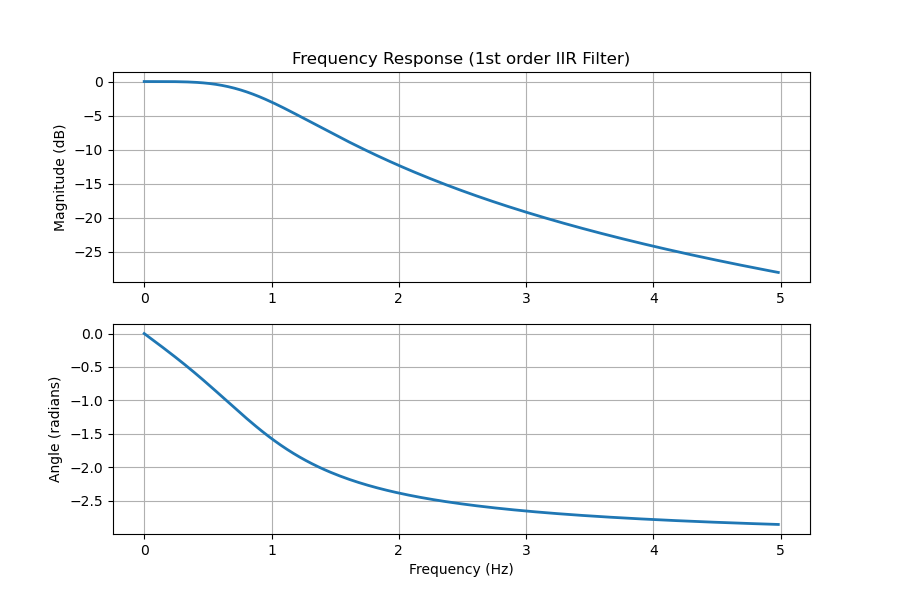
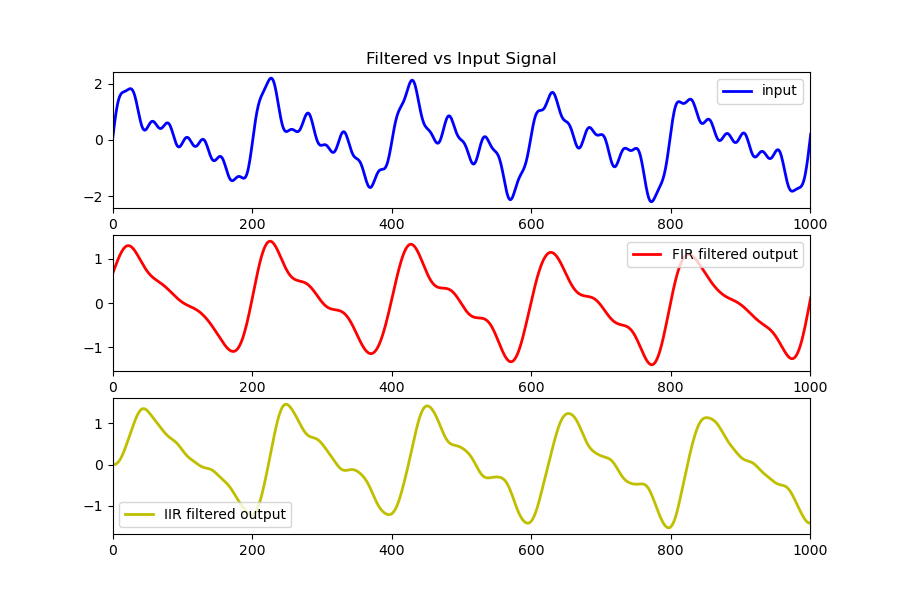
This shows that an IIR filter can preserve the signal’s shape just as well as an FIR filter with fewer taps depending on the restrictions derived from our signal of interest.
