Everything Fails: Design Using Reliability Engineering
If a failure of your design is going to cause anything more than a minor inconvenience, you need to plan for failure. Every system fails sooner or later, the better you plan for it the less damage will occur when failure strikes. Reliability engineering is a well-studied and understood field, but it can often be hard to put those principles into practice.
Aircraft, space and oil and gas drilling systems are excellent examples of high reliability and high availability systems. A complete failure of the flight control system can have catastrophic results, costing the lives of hundreds of passengers.
Reliability is defined as the probability of not failing within a given time period and under specific conditions. The goal of reliability engineering is to increase the reliability of systems as much as possible while staying within the system constraints (e.g., budget, size, power, etc.).
Define the probability of success as R (the reliability) and the probability of failure as F, given that the only two available states are success and failure, we can state that R + F = 1, or alternatively the reliability can be written as 1 - R = F.
Series System Reliability
A system in which sub-systems are connected in series, where the failure if any given component will result in the failure of the system, is defined as a series system. The reliability of two sub-systems in series can be determined by multiplying the reliability of the two sub-systems. The overall reliability of the systems is then equal to:
Rsystem = R1 R2 = (0.9)(0.9) = 0.81 = 81%
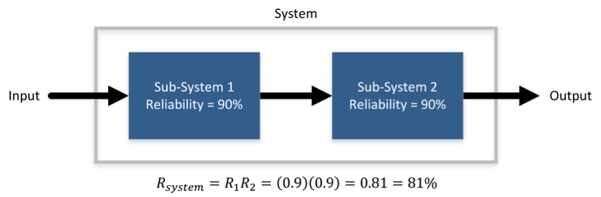
Figure 1: Series system reliability.
A series configuration, as shown in Figure 1 is the most common configuration for most industrial and consumer systems. When designing series systems that cannot practically support redundancy, the key focus is on increasing the reliability of the individual sub-systems. The greatest reliability gains will be achieved by focusing on improving the reliability of the weakest link in the chain.
Redundant System Reliability
In systems where failure can result in catastrophic damage, redundant systems are used to increase the overall reliability. The reliability of two systems in parallel can be defined as:
Rsystem= 1 - F1F2 = 1 - (0.1)(0.1) = 0.99 = 99%, where F = 1 - R
This calculation assumes that the reliability of the voter or switch is 100%. In practice that will never be the case, but it will typically be significantly higher than the individual sub-system reliabilities.
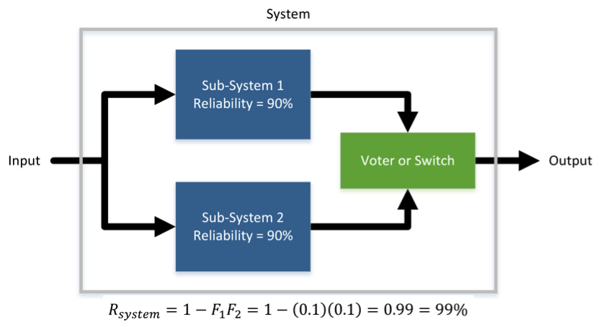
Figure 2: Redundant system reliability.
The role of the voter or switch is to decide which sub-system to use, or to decide whether one of the sub-systems has failed, in which case the failed sub-system will be ignored. Critical aircraft avionics will rely on the redundant system topology shown in Figure 2, often with triple redundancy of the sub-systems. An error in one of the sub-systems will then be outvoted by the other two sub-systems. Given that each sub-system fails rarely, it is expected that the sub-systems will fail independently, and it is highly unlikely that two of the sub-systems will fail simultaneously.
Overall System Reliability
Although redundancy can be used and is often used with good success, care must be taken in designing redundant systems. Redundancy sometimes results in reduced rather than increased reliability. This can be due to poor design of the overall system architecture, a failure in the voting or switching system, or complacency and neglect by the operators who pay less attention to anomalous behavior because of an assumption that the system won’t fail.
All high-reliability systems should undergo thorough testing and validation-one cannot assume that because a system has redundancy that it will be more reliable than a system without redundancy. As with all engineering challenges, a holistic approach must be taken that meets the project requirements for budget, schedule, and performance.
Additional Resources
National Instruments - Redundant System Basic Concepts